No dimensionamento de uma instalação eléctrica de Baixa Tensão existem duas leis que são fundamentais e incontornáveis: a Lei de Ohm e a Lei de Joule. A primeira define o limite mínimo da resistência ou da impedância das cargas ligadas a cada circuito, para cada disjuntor; a segunda define a potência máxima dos receptores por circuito, sem actuação dos respectivos disjuntores. Ambas, em conjunto, permitem estabelecer limites de segurança eléctrica para a canalização eléctrica e respectivos receptores.

14› Cálculos em Circuitos Elétricos
14.1. Lei de Ohm
Em 1827, Georg Simon Ohm enunciou a seguinte lei, à qual foi dada mais tarde o seu nome:
Lei de Ohm – É constante o quociente entre a tensão aplicada a um condutor linear (ou a um receptor resistivo e linear) e a intensidade de corrente que o percorre. A esta constante de proporcionalidade dá-se o nome de resistência elétrica R.
A lei de Ohm é traduzida matematicamente por:
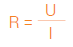
com:
R resistência elétrica (em ohms - Ω)
U tensão aplicada (em volts – V)
I intensidade de corrente (em ampéres – A)
PROBLEMAS - Lei de Ohm
P1 Uma resistência linear é percorrida por uma intensidade de 0,3 A quando submetida a uma tensão de 24 V.
Calcule:
a) O valor da resistência;
b) O valor da intensidade que ela absorveria se lhe aplicássemos uma tensão de 15 V.
P1 Solução
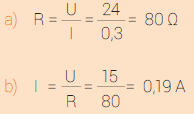
P2 A resistência eléctrica de um aquecedor absorve 3 A quando ligada a 230 V. Calcule o valor da tensão que lhe foi aplicada se ela absorvesse 1,2 A.
P2 Solução
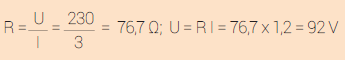
P3 Uma dada resistência de aquecimento de 50 Ω é normalmente ligada a 230 V. Calcule o valor da resistência que deveria ser acrescentada de modo que ela absorvesse 3 A da rede.
P3 Solução
26,7 Ω
P4 Um ferro de engomar absorve 2,5 A quando ligado à rede de 230 V. Qual será a intensidade que absorveria se o ligássemos a 110 V?
P4 Solução
1,2 A
A resistência elétrica de um recetor resistivo e linear tem, portanto, um valor constante, o que quer dizer que se duplicarmos a tensão elétrica aplicada, a intensidade de corrente absorvida também duplicará; se reduzirmos a tensão para metade, a intensidade de corrente absorvida também será metade da anterior. Desta forma, o quociente entre a tensão elétrica e a intensidade de corrente será sempre constante.
14.2. Energia e Potência. Lei de Joule
14.2.1. Efeitos da corrente. Efeito de Joule
A corrente elétrica num condutor ou num receptor produz vários efeitos, nomeadamente: químico, mecânico e térmico.
O efeito químico permite carregar as baterias, funcionando então como acumuladores ou permite efectuar os diferentes processos de galvanoplastia, como o revestimento de peças por camadas de ouro, prata, níquel, platina, e outros.
O efeito mecânico permite o funcionamento dos motores eléctricos que vão transformar a energia elétrica recebida em energia mecânica, que será fornecida pelo veio do motor.
O efeito térmico ou calorífico não é mais do que a transformação de energia eléctrica em energia calorífica, num condutor ou num receptor térmico. A este efeito calorífico da corrente eléctrica dá-se o nome de efeito de Joule, em homenagem ao físico inglês James Joule que primeiro o estudou.
O efeito de Joule nos condutores e nos receptores resulta de choques entre os electrões livres e os átomos das substâncias constituintes dos condutores e dos receptores, sempre que é aplicada ao circuito uma determinada tensão eléctrica. De cada choque resulta, como é fácil de compreender, alguma libertação de calor. Em virtude de serem muitos os electrões em movimento, o calor libertado num condutor ou num receptor pode ser bastante considerável.
O calor libertado que, em muitas circunstâncias, é um inconveniente porque constitui perda de energia pode, no entanto, ser aproveitado em muitas aplicações, nomeadamente: caloríferos, torradeiras, ferros de engomar, etc. – nesta situação, tem uma utilidade, sendo então considerado uma vantagem.
14.2.2. A lei de Joule
A energia eléctrica que se transforma em calor num receptor ou num condutor pode ser quantificada, isto é, podemos calcular o seu valor através de uma expressão matemática, a qual traduz a lei de Joule. Esta lei, enunciada por James Prescott Joule, em 1841, diz o seguinte:
Lei de Joule – “A energia elétrica que se transforma em energia calorífica num recetor (ou num condutor) é diretamente proporcional à resistência elétrica deste, ao quadrado da intensidade de corrente e ao tempo de passagem da corrente”. É traduzida matematicamente pela expressão:

com:
W: energia elétrica transformada em energia calorífica (joules – J)
R: resistência elétrica (ohms - Ω)
I: intensidade de corrente (amperes – A)
t: tempo de passagem da corrente (segundos – s)
14.2.3. Energia e Potência
A lei de Joule diz-nos, entre outras coisas, que a quantidade de energia transformada num receptor depende do tempo durante o qual se processa essa transformação, variando directamente proporcional com o tempo decorrido.
Visto que os receptores não são todos iguais, podemos ter receptores a consumirem a mesma quantidade de energia em intervalos de tempo diferentes. Vejamos alguns exemplos!
Podemos ter as seguintes duas resistências a consumirem o mesmo valor de energia, em intervalos de tempo diferentes:
• Resistência R1
- consome 1.500 J durante 3 s;
• Resistência R2
- consome 1.500 J durante 1,5 s.
Podemos ter os seguintes dois geradores a fornecerem o mesmo valor de energia eléctrica, em intervalos de tempo diferentes:
• Gerador G1 - fornece 1.500 J durante 3 s;
• Gerador G2 – fornece 1.500 J durante 1,5 s.
Podemos ter os seguintes dois motores a fornecerem o mesmo valor de energia mecânica, em intervalos de tempo diferentes:
• Motor M1 – fornece 1.500 J durante 3 s;
• Motor M2 – fornece 1.500 J durante 1,5 s.
O que é que se pode concluir destes exemplos? Bom, embora o valor de energia considerado seja sempre o mesmo, para os diferentes exemplos, os intervalos de tempo de transformação, variam de uns exemplos para outros, isto é, a velocidade de transformação energética é diferente de uns exemplos para outros. Ou seja, a energia fornecida ou consumida, na unidade de tempo (W / t), é variável. Nos exemplos apresentados, temos as duas seguintes situações distintas:
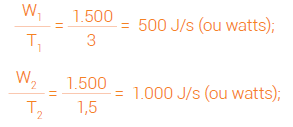
Define-se então o conceito genérico de potência P como a energia absorvida ou fornecida na unidade de tempo. É expressa pela relação:
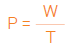
com:
P potência (J/s ou watts – W)
W energia (joules – J)
t tempo (segundos – s)
Temos assim que a resistência R1 absorve 500 W, o gerador G1 e o motor M1 fornecem 500 W; a resistência R2 absorve 1.000 W e o gerador G2 e o motor M2 fornecem 1.000 W. Isto é, R2, G2 e M2 têm maior potência que R1, G1 e M1.
Qual será afinal a grande importância da potência de um receptor ou de um gerador?
Bom, em muitas situações é importante que o valor da potência P seja elevado, porque de outro modo o circuito, o receptor, e os outros, não funciona, pois poderá não ter potência suficiente. Por exemplo, não vamos colocar num automóvel o motor de uma motorizada ou não vamos pôr a levantar pesos e alteres um indivíduo magricelas ou não vamos alimentar os receptores de uma residência com uma bateria, entre outros. Em qualquer dos casos é necessária uma potência mínima.
14.2.4. Unidades de energia e de potência
Vimos já que, no Sistema Internacional de Unidades (S. I.), a energia é expressa em Joules (J) e a potência em watts (W) ou joules/segundo (J/s). Há, no entanto, algumas unidades práticas que são utilizadas com alguma frequência. Vejamos algumas delas!
Como unidade prática de energia utiliza-se frequentemente o watt-hora (Wh) e o quilowatt-hora (kWh). Um watt-hora é a energia fornecida por um gerador ou absorvida por um recetor, com a potência de 1 watt, durante 1 hora:
W = P . t ⇔ 1 Wh = 1 W × 1 h
A relação entre o watt-hora e o joule é a seguinte:
1 watt-hora = 1 watt × 1 hora = 1 W × 3.600 s = 3.600 W.s = 3.600 J ⇔ 1 watt-hora = 3.600 Joules
1 quilowatt-hora é, obviamente, igual a 1.000 watt-hora. Nos motores elétricos, utiliza-se com frequência como unidade prática de potência o cavalo-vapor (C.V.), com a seguinte equivalência:
1 cavalo-vapor = 735,5 watts
Não confundir o cavalo-vapor (C.V.) com o horse-power (H.P.) que também é utilizado (principalmente em Inglaterra) e que vale 746 watts.
As potências dos receptores são muito variáveis, consoante a função a que se destinam, podendo ir de alguns watts a milhares de watts. Vejamos alguns exemplos:
• Resistências eléctricas pequenas: 1/8 W, 1/4 W, entre outros;
• Resistências eléctricas maiores: 50 W, 100 W, 500 W, e outros;
• Lâmpadas de incandescência: 75 W, 100 W, 200 W, entre outros;
• Motores eléctricos: 1 CV, 10 CV, 100 CV, e outros;
• Irradiadores: 750 W; 1.000 W, entre outros.
14.2.5. Potência eléctrica e energia eléctrica de receptores térmicos
A potência eléctrica P de um recetor térmico é definida como o produto da tensão elétrica U aplicada pela intensidade de corrente I absorvida:
P = U I (Watts – W)
Visto que, pela lei de Ohm, temos a relação I = U / R, obtemos então:
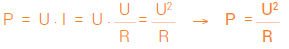
Ou, visto que segundo a lei de Ohm se verifica que U = R I, teremos também:
P = U I = (R I) I = R I2 → P = R I2
Qualquer das três expressões apresentadas permite calcular a potência elétrica absorvida por um recetor térmico de resistência R. Se multiplicarmos a expressão P = R I2 pelo tempo t, obtemos:
W = P t = R I2 t (Joules – J)
fórmula que traduz a lei de Joule já apresentada anteriormente.
Concluímos, portanto, que num recetor térmico toda a energia elétrica é transformada em energia calorífica (W = RI2t), por efeito de Joule, e que a potência elétrica fornecida é toda transformada em potência calorífica (P = R I2).
14.2.6. Potência eléctrica de um motor
No caso dos motores eléctricos, em corrente alternada, a potência P absorvida à rede tem o nome de Potência Activa (absorvida). Esta potência está relacionada com a intensidade de corrente I, pela expressão:
P = U I cos ϕ
em que:
P Potência activa absorvida pelo motor (Watts – W)
U Tensão eléctrica da rede (Volts – V)
I Intensidade de corrente absorvida (Amperes – A)
cos ϕ factor de potência do motor (sem unidades)
O factor de potência do motor tem valores inferiores à unidade – geralmente entre 0,6 e 0,8 – e vem indicado na chapa de características do motor. A potência mecânica que o motor fornece no veio tem o nome de Potência Útil Pu.
14.2.7. Potência e energia, elétricas, de um conjunto de receptores
É fácil de demonstrar que se tivermos ligados no mesmo circuito ou instalação eléctrica um conjunto de receptores (em série, em paralelo ou associação mista), se verifica que:
1) A potência eléctrica total dos receptores é igual à soma das potências individuais:
Pt = P1 + P2 + ... + Pn
2) A energia total consumida pelos receptores é igual à soma das energias consumidas por cada um:
Wt = W1 + W2 + ... + Wn
14.2.8. Perdas. Rendimento
Em qualquer transformação energética, há sempre perdas de energia. As perdas são uma parte da energia que não é utilizada durante o processo de transformação energética que se pretende. Vejamos alguns exemplos!
1) A função do motor elétrico é transformar a energia elétrica em energia mecânica;
2) A função do gerador é transformar, em energia elétrica, outras formas de energia;
3) A função do recetor térmico é transformar energia elétrica em energia calorífica.
Ora, todos sabemos que nem toda a energia absorvida (Wa) será transformada em energia útil (Wu). A diferença entre elas constituirá a energia de perdas Wp = Wa – Wu.
Um motor tem diferentes tipos de perdas: perdas por efeito de Joule nos seus enrolamentos, perdas magnéticas no núcleo de ferro e perdas mecânicas (devido ao atrito do veio, durante a rotação). Um dínamo também tem o mesmo tipo de perdas do motor. Um receptor calorífico, por exemplo, tem perdas reduzidas, pois que a sua função é precisamente a de transformar a energia eléctrica em calorífica – só não utilizará a energia calorífica que se disperse, relativamente à função do recetor.
Define-se rendimento de um receptor ou de um gerador como o quociente entre a energia útil (fornecida) e a energia absorvida:
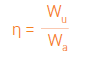
com:
η rendimento (sem unidades)
Wu energia útil (joules)
Wa energia absorvida (joules)
A energia de perdas será: Wp = Wa – Wu.
O rendimento pode também vir expresso em função das potências:
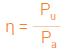
com:
η: rendimento (sem unidades)
Pu: potência útil (joules)
Pa: potência absorvida (joules)
A potência de perdas será: Pp = Pa – Pu.
O rendimento vem normalmente expresso em percentagem, da seguinte forma:

PROBLEMAS - Lei de Joule. Rendimento
P1 Uma torradeira tem as seguintes características: 750 W, 230 V. Calcule:
a) A intensidade que ela absorve;
b) O valor da sua resistência eléctrica;
c) A energia eléctrica que consome (em kWh) durante 20 minutos;
d) A intensidade e a potência absorvidas, se a ligássemos a 150 V.
P1 Resolução

d) A resistência eléctrica da torradeira é constante (70,6 Ω):
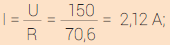
P = U i = 150 x 2,12 = 318 W
ou P = R I2 = 70,6 × 2,122 ≈ 318 W
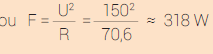
P2 Um motor eléctrico absorve, de uma rede, 5 A quando alimentado a 230 V. Calcule:
a) A potência eléctrica absorvida pelo motor;
b) A potência mecânica (útil) do motor, sabendo que o seu rendimento é de 80%;
c) As perdas totais do motor.
P2 Resolução
-
Pa = U I = 230 × 5 = 1.150 W
-
b) Pu = Pa . η = 1.150 × 0,8 = 920 W
-
c) p = Pa – Pu = 1.150 – 920 = 230 W
P3 Um receptor térmico absorve 1.200 W quando é alimentado a 230 V. Supondo que lhe aplicamos 180 V, calcule:
a) A resistência eléctrica;
b) A intensidade absorvida, a 180 V;
c) A potência absorvida, a 180 V;
d) A energia consumida durante 35 minutos, a 180 V.
P3 Solução
a) 44,2 Ω
b) 4,07 A
c) 732,6 W
d) 427,4 Wh
AUTOR: José V. C. Matias, Licenciado em Engenharia Electrotécnica (IST), Professor do Ensino Secundário Técnico, Autor de livros técnico-didáticos de eletricidade e eletrónica
Fonte: Revista "O Electricista"
