Em português, o termo "resistência" tem dois significados ...
8. Nuvem electrónica. Resistência eléctrica. Ohm
Em português, o termo "resistência" tem dois significados. Resistência é o nome de um componente eléctrico (o receptor atrás referido), mas a oposição feita à corrente pelo componente também se chama resistência. Todos os materiais oferecem resistência à passagem da corrente, uns mais que outros, dependendo da sua constituição e da sua forma. Os electrões que asseguram a corrente eléctrica num condutor eléctrico libertaram-se dos átomos a que pertenciam e circulam pelo material em grande quantidade, como se de uma nuvem electrónica se tratasse (figura 21).

O seu movimento não se verifica apenas num sentido, havendo electrões que se deslocam num sentido enquanto outros se deslocam em sentidos variados. No entanto, existe um sentido preferencial que é seguido pela maioria e que é do ponto onde existe maior concentração de electrões (pólo negativo) para onde a concentração é menor (pólo positivo). A resistência resulta de os electrões não se poderem deslocar livremente pois no seu caminho encontram outros electrões e átomos. Daqui resultam choques com perdas de energia, o que significa resistência, já que o fluxo de electrões é diminuído por estes factos. Se um receptor oferecer mais resistência que outro, a corrente será menor, o que é intuitivo. Esta nova grandeza eléctrica representa-se pelo símbolo R e a unidade SI chama-se Ohm (lê-se "oum") (símbolo Ω) (homenagem ao físico alemão George Ohm (1787-1854)). A grande quantidade de grandezas e unidades usadas em electricidade levou a que se usem, além das letras do alfabeto latino, letras do alfabeto grego. Uma delas é o Ω. É uma letra maiúscula chamada "ómega". No entanto, o símbolo Ω toma o nome da unidade e lê-se "oum".
9. Circuito aberto e circuito fechado
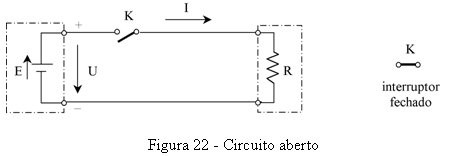
O circuito da figura anterior funciona, mas para interromper o seu funcionamento é preciso desligar um fio da fonte. É mais prático usar um aparelho de corte e comando chamado interruptor. Na figura 22 está representado pela letra K, junto ao seu símbolo. É normal representar o circuito no seu estado de repouso (desligado). Assim, o interruptor está aberto, interrompendo o circuito e a corrente não pode passar (I = 0 A). Diz-se que também o circuito está aberto. Para fornecer corrente à carga é preciso fechar o interruptor, estabelecendo a ligação entre a fonte e o receptor. Nesse caso diz-se que o circuito está fechado.
10. Lei de Ohm
10.1. I como função de U
De acordo com esta lei, a intensidade de corrente que percorre uma resistência é directamente proporcional à tensão aplicada à resistência e inversamente proporcional ao valor desta.
Quer isto dizer que a intensidade de corrente é tanto maior quanto maior for U e quanto menor for R. Se a tensão for grande existe uma grande “pressão” sobre os electrões, o que origina um maior fluxo destes (maior intensidade de corrente). Se houver pouca oposição à corrente (valor pequeno da resistência eléctrica) o valor da intensidade será grande.
Matematicamente esta lei exprime-se através da seguinte equação:
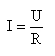
Vejamos alguns exemplos para esclarecer o significado desta afirmação.
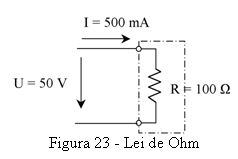
Suponhamos que é aplicada uma tensão de 50 V a uma resistência de 100 Ω (figura 23).
A resistência será percorrida por uma corrente com a intensidade I:
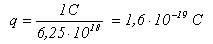
Se aumentarmos a tensão para o dobro, U = 100 V, a corrente na mesma resistência de 100 Ω será I = 1 A, que é o dobro do valor anterior.
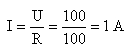
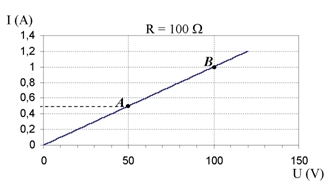
Pode desenhar-se um gráfico para analisar a lei de Ohm, considerando em abcissas a tensão U (variável independente) e em ordenadas a intensidade de corrente I (variável dependente), mantendo constante a resistência R = 100 Ω (figura 24).
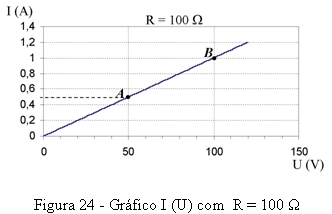
Ao primeiro exemplo numérico ( U = 50 V ; I = 0,5 A) corresponde o ponto A no gráfico. Ao segundo exemplo numérico ( U = 100 V ; I = 1 A) corresponde o ponto B. Observa-se que o gráfico é uma linha recta (gráfico linear), o que resulta da função matemática I = U / R, em que R é constante. É possível determinar, a partir do gráfico, qual é o valor de I correspondente a qualquer valor de U. Por exemplo, para U = 60 V, o valor de I é 0,6 A ou 600 mA.
10.2. Determinação do valor da resistência
Suponhamos agora que consideramos uma resistência com outro valor, por exemplo 200 Ω. Deixamos como exercício o cálculo de I para U = 50 V e para U = 100 V. Obter-se-á, respectivamente, I = 250 mA e I = 500 mA. O gráfico correspondente a R = 200 Ω está representado na figura 25 juntamente com o correspondente a R = 100 Ω. Verifica-se que ambos são rectas, como seria de esperar, mas a inclinação delas é diferente. O correspondente à resistência maior (R = 200 Ω) é mais inclinado para o eixo das tensões que o correspondente à menor resistência (R = 100 Ω). Quanto maior for o valor de uma resistência, mais inclinado é o gráfico sobre o eixo das abcissas.
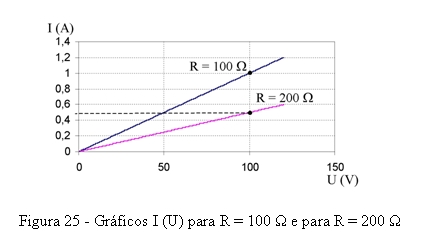
Vimos que para cada valor de R o gráfico apresenta um determinado declive. Quer isto dizer que o declive define o valor da resistência. Isto resulta de outra forma de analisar a lei de Ohm.
Colocando a expressão da lei de Ohm na forma seguinte
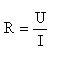
Conclui-se que o quociente entre a tensão U e a intensidade de corrente I é constante e que essa constante é a resistência R. Por isso, é possível determinar o valor de uma resistência a partir dos valores de U e de I. É o que acontece quando pretendemos determinar experimentalmente o valor de uma resistência. Medimos o valor da tensão U aplicada à resistência e o valor da intensidade de corrente I que a percorre e obtemos o valor de R determinando o quociente U / I.
10.3. I como função de R . Resistência variável: reóstato
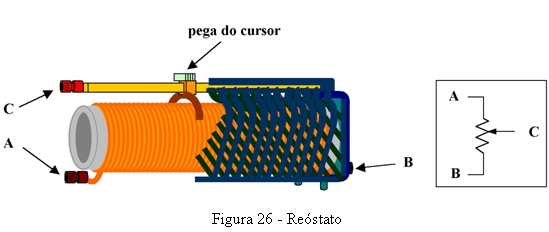
A primeira fórmula da lei de Ohm (ver 10.1) permite-nos ainda outra análise. Para a fazer precisamos de uma resistência cujo valor possa ser modificado. É o caso do reóstato. Este aparelho é constituído por um fio condutor enrolado em torno dum tubo cerâmico e permite variar o valor da resistência através duma peça chamada cursor que está assente no fio e pode deslizar sobre ele. Na figura 26 mostra-se uma imagem e o símbolo dum reóstato. Para permitir visualizar o interior do reóstato, foi retirado o invólucro da parte esquerda. Os pontos A e B são as extremidades da resistência e o ponto C é o cursor. Se deslocar o cursor para cima (no símbolo), a resistência entre A e C diminui e a resistência entre B e C aumenta.
Dos três terminais do reóstato vamos apenas usar o cursor e um dos outros dois (figura 27). Na figura representa-se também o trajecto seguido pela corrente.
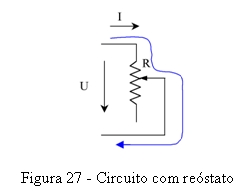
Se colocarmos o cursor na extremidade inferior, a resistência inserida no circuito é máxima. Por isso, a corrente é mínima. Deslocando o cursor para cima a resistência vai diminuindo enquanto a corrente vai aumentando de acordo com a expressão I = U / R. Com o cursor na extremidade superior a resistência será 0, o que implica uma corrente infinita ! Se não há resistência, não há oposição à corrente e é por isso que a corrente é infinita. Este é um valor teórico. Na prática isto não é possível, pois não há uma fonte de alimentação que possa fornecer uma tal corrente. O resultado prático de tal situação seria a deterioração da fonte e a consequente abertura do circuito ou o accionamento de alguma protecção do circuito para esta situação e que abriria o circuito antes que a corrente deteriorasse os seus componentes.
Se registarmos os valores de I obtidos durante a experiência que descrevemos, podemos desenhar um gráfico I(R) (gráfico de I em função de R).
É o que se mostra na figura 28 que corresponde à aplicação de uma tensão de 10 V a uma resistência variável com valor máximo igual a 200 Ω. O gráfico mostra como varia a intensidade de corrente que atravessa a resistência quando o valor desta é modificado com a deslocação do cursor.
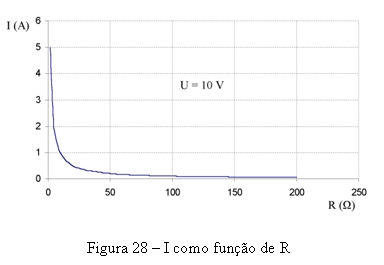
Analisemos esta curva com mais pormenor. Para isso vamos calcular os valores de I para os seguintes valores de R: 200 Ω , 150 Ω , 100 Ω , 50 Ω e 0 Ω. Para o primeiro valor será
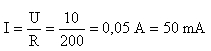
Fica como exercício fazer os restantes cálculos, com os quais obteremos os correspondentes valores de I. Com todos estes valores preenchemos o quadro da figura 29 para facilitar a leitura.

A primeira linha do quadro corresponde ao cursor na posição inferior (R máx). O valor de R é 200 Ω e o valor de I é 50 mA. Na segunda linha o cursor está na posição de três quartos do valor máximo, a que corresponde uma resistência de 150 Ω e uma corrente de 66,(6) mA (a representação (6) significa uma dízima infinita : 66,(6) = 66,6666666.....). E assim sucessivamente para as restantes linhas do quadro. Na última linha usa-se o símbolo ∞ para representar infinito.
Ao reduzirmos a resistência de 200 Ω para 150 Ω (redução de um quarto do seu valor máximo: 200 / 4 = 50 Ω) o aumento da intensidade de corrente é 66,(6) - 50 = 16,(6) mA. Ao reduzir a resistência de 150 Ω para 100 Ω (redução de outro quarto) o aumento da corrente é 100 - 66,(6) = 33,(3) mA , que é o dobro do anterior. A mesma diminuição da resistência provocou o dobro do aumento da intensidade de corrente. A diminuição de outro quarto da resistência, de 100 Ω para 50 Ω provoca um aumento da corrente de 200 - 100 = 100 mA que é 6 vezes maior que no primeiro caso. Reduzindo novo quarto da resistência (de 50 Ω para 0 Ω) a corrente sofre um aumento infinito (de 200 mA para ...).
Conclui-se que a mesma diminuição de resistência produz aumentos de corrente cada vez maiores, o que se deve ao facto de a corrente I ser inversamente proporcional à resistência e resulta da expressão I = U / R, em que R está em denominador. É importante ter este facto presente quando se manuseiam reóstatos, pois uma pequena variação da resistência próximo da extremidade com menor resistência produz grandes aumentos da corrente, ao contrário do que sucede quando se varia a resistência próximo da extremidade do reóstato que corresponde a maior resistência inserida no circuito.
Estes factos são particularmente evidentes na curva da figura 28. Observe-se que de 200 Ω a 50 Ω a variação de corrente é bastante pequena (vimos pelo cálculo que é 200 - 50 = 150 mA). De 50 Ω até 0 Ω a curva tem uma grande alteração correspondente a um enorme aumento da corrente.
Para terminar, note-se que o gráfico só mostra valores de intensidade até 5 A (correspondente a uma resistência de 10 / 5 = 2 Ω), pois para valores menores de R a intensidade de corrente é tão alta que obrigaria a desenhar um gráfico enorme ou a aumentar a escala do eixo de I de tal forma que os valores de I para valores de R maiores pareceriam nulos.
10.4. U como função de I
É possível dar outra forma às expressões da lei de Ohm. Escrevendo U em função de I obtemos, a partir de qualquer das expressões anteriores (ver 10.1 e 10.2), a equação
U = R · I
Se uma resistência R inserida num circuito for percorrida por uma corrente I, a tensão U aos seus terminais é directamente proporcional a I. Esta é outra forma de enunciar a lei de Ohm associada à expressão anterior.
Se, por exemplo, uma resistência R = 50 Ω for percorrida por uma corrente de 20 mA, a tensão aos seus terminais é U = R I = 50 x 0,020 = 1 V.
Do que vimos, conclui-se que existe uma relação entre o valor duma resistência, o valor da tensão aos seus terminais e o valor da intensidade de corrente que a percorre. Essa relação pode exprimir-se matematicamente por qualquer uma das seguintes expressões equivalentes:
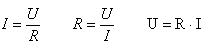
SOLUÇÃO
(Resolução do exercicio proposto no numero anterior)
EXERCÍCIO 4
q = 1,6 X 10-19 C (carga do electrão)
Q = I x t = 0,001 x 1 = 0,001 C (carga transportada por 1 mA durante 1 s)
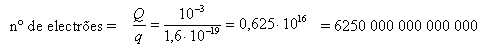
Exercícios propostos (Soluções no próximo número):
Exercício 5
O fio de uma resistência de aquecimento tem uma resistência com o valor de 48,4 Ω. Qual o valor da intensidade de corrente que percorre a resistência quando lhe for aplicada uma tensão de 220 V? E se a tensão aplicada for 380 V?
Exercício 6
Uma lâmpada para uma lanterna de bolso tem as indicações 2,5 V / 0,2 A. Determinar o valor da resistência do filamento da lâmpada.
Exercício 7
Uma resistência de 150 Ω é percorrida por uma corrente com intensidade igual a 20 mA. Qual o valor da tensão aos seus terminais?
AUTOR: Jorge Castilho Cabrita - Engenheiro Electrotécnico (IST)
