Associações de resistências em paralelo e mista. Este artigo completa o estudo das associações de resistências iniciado no número anterior, com uma análise teórica e exemplos de aplicação.
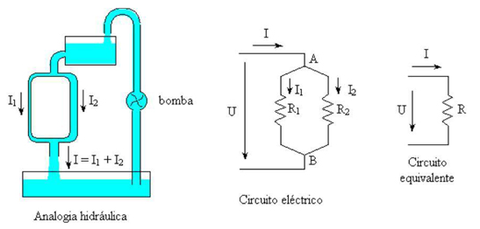
13 - Associação de resistências em paralelo
13.1 – Divisão de corrente
Na analogia hidráulica com a associação de resistências em paralelo representada na figura 38, observa-se que a água saída do depósito superior tem duas vias por onde se pode escoar.
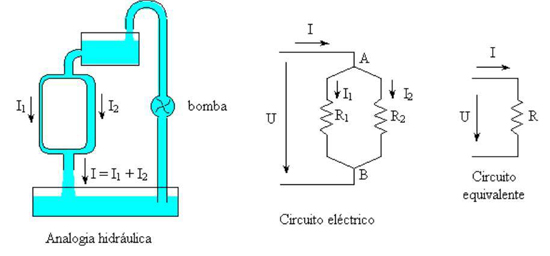
Figura 38 – Associação de resistências em paralelo
As duas vias estão sujeitas à mesma pressão da água, mas não são iguais, sendo uma mais estreita que a outra. Por isso, circulará mais corrente de água pela via mais larga, já que esta, por ter maior secção, oferece menor resistência à sua passagem. Naturalmente que a corrente que sai do tanque superior é igual à soma das correntes que passam nas duas vias e é também igual à corrente que passa na via inferior para o tanque inferior (I = I1 + I2). Embora sendo fenómenos diferentes, passa-se uma situação análoga no circuito eléctrico. Ambas as resistências estão sujeitas à mesma tensão. A corrente I fornecida pela fonte de alimentação bifurca-se no ponto A (nó), dando origem a duas correntes I1 e I2 que atravessam as resistências R1 e R2, respectivamente. O valor da intensidade de cada uma destas correntes depende do valor da resistência, sendo maior na resistência de menor valor. Uma das características da associação de resistências em paralelo é que a intensidade de corrente total I é a soma das intensidades de corrente em cada uma das resistências (I = I1 + I2) (há uma divisão da corrente). Outra característica é que as duas resistências estão sujeitas à mesma tensão aplicada U, devido a que os pontos A e B são comuns às duas resistências.
13.2 - Resistência equivalente
É possível substituir uma associação de resistências em paralelo por um circuito com uma só resistência equivalente R (figura 38). O valor de R deve ser tal que, aplicando-lhe a mesma tensão U que é aplicada à associação de resistências, a intensidade de corrente I que atravessa R seja igual à intensidade de corrente total I na associação. Determina-se o valor de R por aplicação da lei de Ohm e da expressão anterior I = I1 + I2.
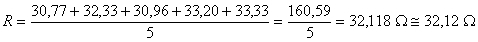
O valor de R é o inverso do indicado no primeiro membro da equação.
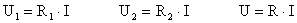
Antes de continuar, vejamos um exemplo numérico. Se R1 = 10 Ω e R2 = 20 Ω, o valor de R será :
Note-se que o valor de R é menor que o de qualquer das resistências R1 ou R2.
No caso de haver um maior número de resistências em paralelo, será I = I1 + I2 + ... + In, em que n é o número de resistências. De forma análoga à anterior obter-se-à:
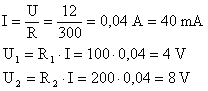
Consideremos, como exercício, uma associação em paralelo das resistências R1 = 20 Ω, R2 = 40 Ω e R3 = 80 Ω. O valor da resistência equivalente R obtém-se dos seguintes cálculos:
No caso particular das n resistências terem o mesmo valor, R1 = R2 = ... = Rn, o valor de R será:
Note-se, de acordo com este resultado, que o valor da resistência equivalente a duas resistências iguais em paralelo é metade do valor da resistência de qualquer delas. Se forem três resistências iguais em paralelo, a resistência equivalente é um terço de qualquer delas e assim sucessivamente.
Como exercício suponhamos que temos uma associação em paralelo de 10 resistências iguais com um valor de 50 Ω. O valor da resistência equivalente à associação é
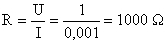
13.3 - Shunt de um amperímetro
A palavra inglesa shunt (lê-se "chante") está muito divulgada na gíria electrotécnica apesar de existir o equivalente em português que é paralelo ou derivação. Tal como no voltímetro é possível obter vários campos de medida com o mesmo aparelho, colocando resistências em série com o circuito de medida, também é possível ter vários campos de medida com o mesmo amperímetro, colocando resistências em paralelo com o circuito de medida. É o que se representa na figura 39.
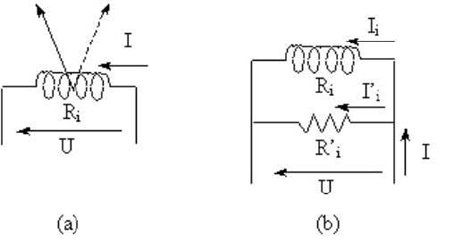
Figura 39 – Shunt de um amperímetro
Suponhamos que o ponteiro se desloca para o final da escala quando a bobina (com resistência Ri = 1 Ω), é percorrida por uma corrente com a intensidade de 10 mA (figura 39 (a)). Para que o aparelho possa medir correntes com intensidades até, por exemplo, 30 mA, a corrente de intensidade igual a 20 mA (resultante da diferença 30-10 = 20 mA) deverá percorrer a resistência R'i em paralelo com Ri (figura 39 (b)). Calculemos o valor desta resistência por aplicação da lei de Ohm. Para isso vamos precisar de saber o valor da tensão U aos seus terminais, o que se pode determinar a partir de Ri, já que a tensão U é a mesma para as duas resistências. Chamemos Ii à intensidade de corrente em Ri e I'i à intensidade de corrente em R'i. Se quisermos adicionar outro campo de medida ao amperímetro, colocamos outra resistência em paralelo com Ri. Esta resistência deverá ser percorrida pelo excesso de corrente, de tal forma que Ri não seja percorrida por uma intensidade superior à sua capacidade que é, neste exemplo, 10 mA. E assim sucessivamente para mais campos de medida.
Nota: Partindo do princípio de que os conceitos associados aos valores das grandezas estão já assimilados e para simplificar a leitura do texto, vamos normalmente substituir, a partir daqui, a expressão "valor da intensidade da corrente eléctrica" por "corrente", pressupondo que são equivalentes. O mesmo faremos em relação às expressões associadas aos valores de outras grandezas. Por exemplo, em vez de "valor da tensão eléctrica", diremos apenas "tensão". Em termos orais, muitas vezes se fala assim.
14 - Associação mista de resistências
Com um mínimo de três resistências é possível reunir os dois tipos de associação já conhecidos. Os casos mais simples estão representados na figura 40.
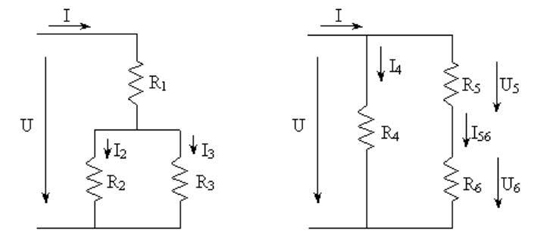
Figura 40 – Associações mistas de resistências
Um dos circuitos da figura 40 é constituído por uma resistência R1 em série com uma associação em paralelo das resistências R2 e R3.
O outro circuito da mesma figura é constituído por uma associação em paralelo da resistência R4 com a associação em série das resistências R5 e R6.
O cálculo das diversas grandezas associadas a cada um dos circuitos faz-se de maneira análoga aos estudos já efectuados com as associações em separado.
Consideremos U=100 V, R1 = 50 Ω, R2 = 100 Ω, R3 = 150 Ω.
Para facilitar a resolução, vamos substituir a associação de R2 com R3 pela resistência equivalente R23 (figura 41 (b)).
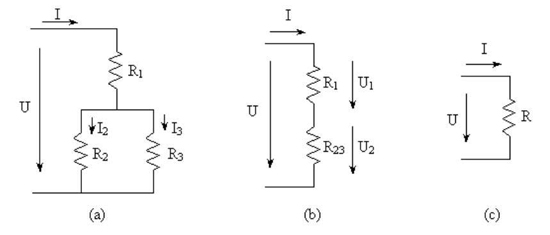
Figura 41 – Determinação dos valores das correntes e das tensões
Cálculo da resistência equivalente R
Calculemos primeiro o valor de R23.
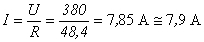
O cálculo de R resulta do facto de R1 estar em série com R23.
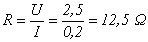
Cálculo das correntes
Note-se que a corrente em R1 é I e que já é possível calcular o seu valor. De facto, I pode ser calculada por duas vias. Uma é sabendo U1 e R1, mas não sabemos U1. Outra via é sabendo U e R, pois a corrente que percorre R1 (figura 41(a) ou (b)) é a mesma que percorre R (figura 41 (c)).
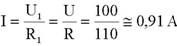
Para calcular I2 e I3 é preciso saber o valor da tensão U2 (figura 41 (b)) aos terminais de R23.
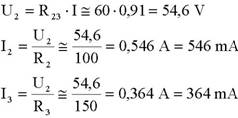
Pode-se verificar o valor de I = I2 + I3 = 0,546 + 0,364 = 0,91 A = 910 mA. Como seria de esperar, obtivemos o mesmo valor que já tínhamos determinado.
Cálculo de U1
Finalmente, vamos calcular o valor de U1, o que pode ser feito por dois processos.
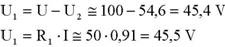
Existe uma diferença de 0,1 V entre os dois valores, resultante da aproximação efectuada atrás no cálculo de I. Situações de aproximações são correntes nos cálculos, já que, muitas vezes, não é possível usar o valores exactos, como no caso das dízimas e outras vezes não se torna prático. Para saber se o erro cometido neste caso é importante, pode determinar-se o seu valor em percentagem:
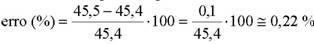
Trata-se de um erro muito pequeno. Se quisermos esclarecer com mais rigor o valor de U1, devemos efectuar o cálculo sem aproximar o valor de I e então obtemos:
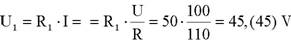
Este é o valor exacto de U1.
Vamos agora calcular os valores das grandezas para o segundo circuito de associação mista. Tal como fizemos para o circuito anterior, vamos repetir aqui o esquema na figura 42 (a) ao lado do esquema equivalente da figura 42 (b) (com R56 equivalente a R5 em série com R6) e do esquema equivalente da figura 42 (c) (com R equivalente a R4 em paralelo com R56).
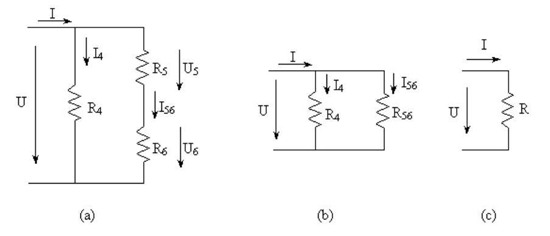
Figura 42 – Determinação dos valores das correntes e das tensões
Tomemos os seguintes valores: U = 100 V ; R4 = 20 Ω ; R5 = 40 Ω ; R6 = 80 Ω.
Cálculo da resistência equivalente R
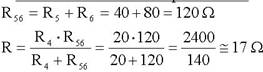
Cálculo das correntes
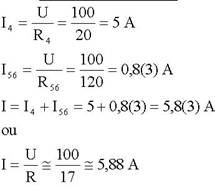
Na última expressão obtém-se um valor R um pouco diferente do anterior, o que é devido à aproximação efectuada antes no cálculo de R.
Tal como no circuito anterior, é possível calcular o valor exacto de I da seguinte forma:
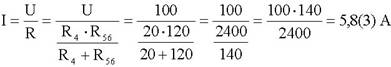
14.1 - Divisor de tensão em vazio e em carga
Já utilizámos anteriormente o termo carga de uma fonte de alimentação como sendo um receptor a ela ligado e de quem recebe corrente. Quando não há carga ligada à fonte diz-se que esta está em vazio.
Estes mesmos conceitos se aplicam a um divisor de tensão. Na figura 43 representa-se o divisor de tensão em vazio, já estudado nos pontos 12.1 e 12.2 sobre associação de resistências em série.
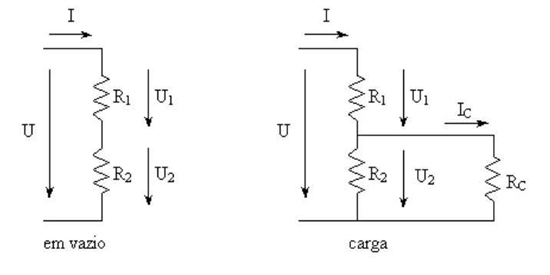
Figura 43 - Divisor de tensão
Em vazio
Como então se calculou, sendo dados os valores de U = 24 V, R1 = 12 Ω , R2 = 48 Ω, obtém-se:
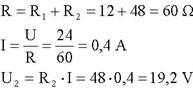
Em carga
Calculemos agora o valor de U2 no circuito do divisor de tensão em carga, sendo dados os valores de U, R1 e R2. Note-se que este circuito é uma associação mista de resistências. Pode-se calcular U2 a partir de U2 = U-U1.
Para determinar o valor de U1 é preciso calcular I (porque U1 = R1 x I)e para saber I determina-se primeiro a resistência equivalente à associação (porque I = U / R, sendo R a resistência equivalente).
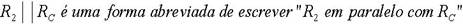
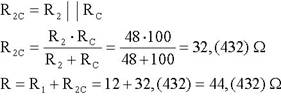
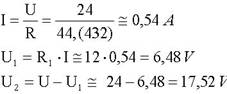
Conclui-se que a tensão U2 é maior em vazio do que em carga, devido ao aumento de U1, por causa do aumento de I.
Resolução do exercício proposto no número anterior :
Exercício 8
I = 1 mA = 0,001 A
UB = RB x I = (100 + 900 + 2000) x 0,001 = 3000 x 0,001 = 3 V
UC = RC x I = (RB + 7000) x 0,001 = (3000 + 7000) x 0,001 = 10000 x 0,001 = 10 V
UD = RD x I = (RC + 20000) x 0,001 = (10000 + 20000) x 0,001 = 30000 x 0,001 = 30 V
UE = RE x I = (RD + 70000) x 0,001 = (30000 + 70000) x 0,001 = 100000 x 0,001 = 100 V
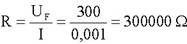
R''i = R - RE = 300000 - 100000 = 200000 Ω = 200 K Ω
Exercícios propostos (Solução no próximo número):
Exercício 9
Calcular a resistência equivalente à associação em paralelo das resistências de 5,6 KΩ, 3,3 KΩ e 22 KΩ.
Exercício 10
Escrever a expressão mais simples correspondente ao valor da resistência medida pelo ohmímetro no seguinte circuito.
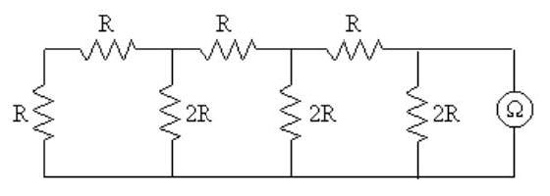
(Este circuito faz parte de outro circuito chamado "Conversor digital-analógico R-2R")
Exercício 11
Por que razão a tensão U2 no divisor de tensão em carga é menor que no divisor de tensão em vazio (figura 43)?
AUTOR:Jorge Castilho Cabrita, Engenheiro Electrotécnico (IST), Professor do Ensino Secundário
