II - Corrente contínua

O nosso estudo aborda os métodos de medida da tensão, intensidade de corrente e resistência eléctricas continuando com a análise das características da associação de resistências em série e sua aplicação num caso concreto.

11 – Medição de grandezas eléctricas

11.1 – Aparelhos de medida

A medida das grandezas eléctricas é feita com aparelhos de medida adequados.

Já falámos anteriormente na medida da tensão entre dois pontos dum circuito, assim como na medida da intensidade de corrente que percorre uma resistência. A medida da tensão é efectuada com um aparelho designado voltímetro e a medida da intensidade de corrente é feita com um amperímetro. Há aparelhos de medida analógicos e digitais. Nos analógicos a leitura é efectuada através da comparação da posição dum ponteiro com as divisões duma escala, tal como nos relógios com ponteiros. Nos digitais a leitura é directa no visualizador. Na figura 30 mostram-se fotografias de um voltímetro, de um amperímetro e de um ohmímetro analógicos assim como de um multímetro digital. Chama-se ohmímetro a um aparelho capaz de medir resistências. Como o nome sugere, um multímetro destina-se a efectuar múltiplas medidas. É um aparelho combinado. Os multímetros vulgares medem tensões, intensidades de corrente e resistências. Muitos multímetros podem medir também outras grandezas eléctricas de que ainda não falámos, como a capacidade, a frequência e o ganho de corrente de transístores. Na imagem do multímetro vêem-se duas pontas de prova. São dois condutores eléctricos. Cada um termina, numa extremidade, numa peça chamada ficha macho (banana) que é inserida num alvéolo (fêmea) do multímetro. Na outra extremidade encontra-se uma peça ponteaguda destinada a tocar num dos pontos do circuito. A ponta de prova preta é ligada ao alvéolo comum (negativo) do multímetro e a vermelha é ligada a um do outros alvéolos (positivo).

Figura 30 – Aparelhos analógicos : Voltímetro , Amperímetro , Ohmímetro

Aparelho digital : Multímetro

11.2 – Medida da tensão

A medida da tensão aos terminais duma resistência é feita ligando o voltímetro aos seus terminais, de forma que os pólos sejam ligados como se mostra na figura 31. O pólo positivo é o vermelho e o negativo é o preto.

Figura 31 – Medida da tensão com voltímetro

11.3 – Medida da intensidade de corrente

A medida da intensidade de corrente que atravessa uma resistência é feita inserindo o amperímetro no circuito de forma a ser percorrido pela mesma corrente que atravessa a resistência, como se mostra na figura 32.

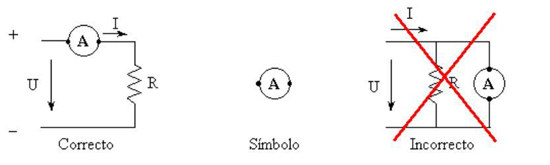
Figura 32 – Medida da intensidade de corrente com amperímetro

11.4 – Medida da resistência

Há vários métodos para medir o valor duma resistência.

11.4.1 – Método directo: uso de ohmímetro

O método directo é o mais simples. Consiste na utilização dum ohmímetro que se liga aos terminais da resistência como se mostra na figura 33. Existem aparelhos que apenas medem a resistência (ohmímetros, como se disse), mas é mais frequente usar multímetros com a mesma finalidade, pois torna-se mais económico, já que o multímetro pode efectuar outros tipos de medidas.

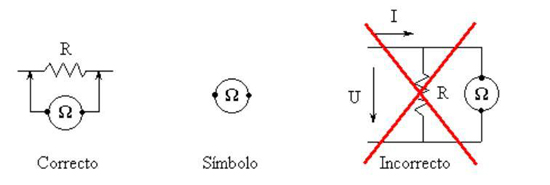
Figura 33 – Medida da resistência com ohmímetro

11.4.2 – Métodos indirectos. Método volt-amperimétrico

No estudo da lei de Ohm referimos a possibilidade de medir o valor duma resistência R a partir das medidas da tensão U aos seus terminais e da intensidade de corrente I que a percorre, o que pode ser feito com um voltímetro e um amperímetro montados como se mostra na figura 34.

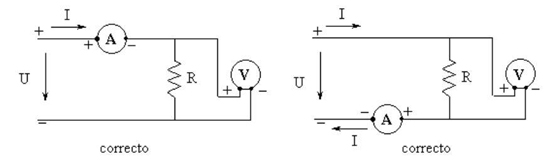
Figura 34 – Medida da resistência pelo método volt-amperimétrico

O valor de R resulta, como se disse, da expressão R = U / I. É o chamado método volt-amperimétrico de medida de uma resistência.

Convém, no entanto, fazer várias medidas de pares de valores (U, I) para determinar a média dos valores dos quocientes correspondentes. A razão é que o resultado dos vários quocientes U / I deverá ser igual, mas o mais provável é haver pequenas diferenças resultantes de erros efectuados nas medidas. Realizando a média é mais provável encontrarmos um valor próximo do verdadeiro.

Para exemplificar, suponhamos que realizamos os seguintes 5 pares de medidas (U, I ).

U (V)	I (A)	R (Ω)
10	0,325	30,77
15	0,464	32,33
20	0,646	30,96
25	0,753	33,20
30	0,900	33,33

O valor mais provável de R será, a partir destas medidas, o resultado da média aritmética dos valores de R indicados no quadro e obtidos por aplicação da lei de Ohm.

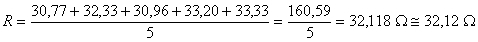
Quando se pretende obter grande precisão na medida da resistência pode utilizar-se outro método indirecto baseado na chamada ponte de Wheatstone, como se verá noutra ocasião.

12 - Associação de resistências em série

12.1 - Divisão de tensão

É usual encontrarem-se em electricidade agrupamentos de resistências. Um deles consiste em ligar uma extremidade duma resistência a uma extremidade da outra (figura 35).

Façamos uma analogia hidráulica para facilitar a compreensão das características desta associação.

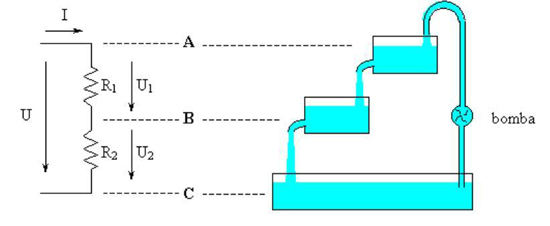
Figura 35 - Associação de resistências em série . Analogia hidráulica

A bomba de água eleva a energia potencial da água ao transportá-la para o depósito superior, o que corresponde à tensão eléctrica U entre os pontos A e C. A energia potencial adquirida pela água no depósito superior obriga a que a água caia para o depósito intermédio onde a energia potencial é menor. Esta queda da água é feita à custa de uma queda da sua energia potencial, pois uma parte da energia potencial é transformada na energia cinética da água em movimento. No nosso circuito eléctrico, a tensão U origina uma corrente eléctrica de intensidade I que atravessa sucessivamente R1 e R2, com o sentido indicado pela seta. O ponto A está a um potencial eléctrico maior que o ponto B. Entre os pontos A e B dá-se uma queda da tensão U1 que é igual à diferença dos potenciais entre A e B. A passagem da água do depósito intermédio para o inferior faz perder o resto da energia potencial. No depósito inferior a energia potencial de referência é nula. No circuito eléctrico a passagem da corrente de B para C é acompanhada de uma queda da tensão U2. O potencial é nulo no ponto C. Desta forma, a tensão total U é a soma das tensões U1 e U2. Quanto à corrente, a que atravessa R1 é a mesma que atravessa R2. Só há uma corrente I no circuito. São estas as características da associação série.

Pelo facto de a tensão total U se repartir pelas duas resistências, este circuito também é designado por divisor de tensão.

12.2 - Resistência equivalente

É possível considerar uma resistência R que tenha o mesmo comportamento eléctrico que a associação das duas resistências, de forma que possa substituí-las. Esta resistência R chama-se resistência equivalente. Para que o comportamento eléctrico seja igual, a intensidade de corrente que percorre R quando lhe é aplicada a tensão U deve ter o mesmo valor que a intensidade de corrente que percorre a associação quando lhe é aplicada a mesma tensão U (figura 36).

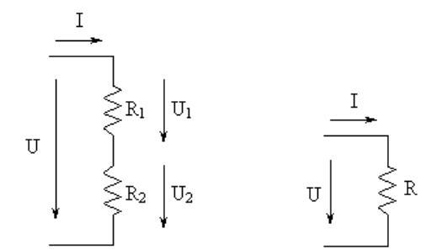
Figura 36 - Resistência equivalente

Vamos determinar qual o valor que deve ter R para satisfazer aquela condição. Obtemos o valor de R por aplicação da lei de Ohm às três resistências:

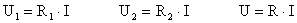
Sabendo que U = U1 + U2 e substituindo os valores das tensões pelas expressões anteriores, obtém-se:

É possível simplificar a expressão devido a I aparecer em todas as parcelas. Basta dividir todas as parcelas pelo mesmo número I. Obtém-se assim o valor de R:

R = R1 + R2

Como exemplo de aplicação, suponhamos que R1 = 100 Ω e que R2 = 200 Ω, sendo U = 12 V a tensão aplicada à associação. Pretende-se determinar o valor da resistência R equivalente, assim como as tensões U1 e U2.

O valor de R determina-se fazendo R = R1 + R2 = 100 + 200 = 300 Ω.

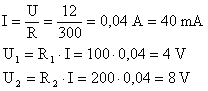
Para determinar U1 e U2 é necessário saber o valor de I e substituí-lo nas expressões de U1 e U2.

Como seria de esperar, verifica-se que U = U1 + U2 = 4 + 8 = 12 V

Se a associação for composta por várias resistências, o valor da resistência equivalente determina-se de modo semelhante. Sendo n o número de resistências em série, obter-se-á:

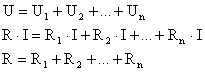
Por exemplo, a resistência equivalente à associação em série das resistências de 20 Ω, 40 Ω e 60 Ω tem o valor R = 20 + 40 + 60 = 120 Ω.

No caso particular de as resistências serem todas iguais, o valor de R será:

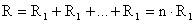
Por exemplo, a resistência equivalente à associação em série de 5 resistências de 20 Ω, tem o valor R = 5 x 20 = 100 Ω.

12.3 - Resistência adicional de um voltímetro

A parte eléctrica de um voltímetro analógico é constituída por um fio de pequena resistência enrolado em bobina, em série com uma resistência de valor elevado. Na figura 37a representa-se apenas a bobina e o ponteiro que lhe está associado (a cheio). Supondo que a bobina tem uma resistência Ri de 100 Ω e que o ponteiro se desvia para o final da escala (a tracejado) quando o fio da bobina é percorrido por uma corrente de intensidade igual a 1 mA, a tensão medida pelo aparelho é U = Ri I = 100 x 0,001 = 0,1 V. Este aparelho não pode medir uma tensão superior a 0,1 V. Para que ele possa medir uma tensão superior é preciso associar-lhe em série uma resistência R'i (lê-se "R linha") (figura 37b). Vamos calcular o valor que deve ter R' i para que o aparelho possa medir tensões até 1 V.

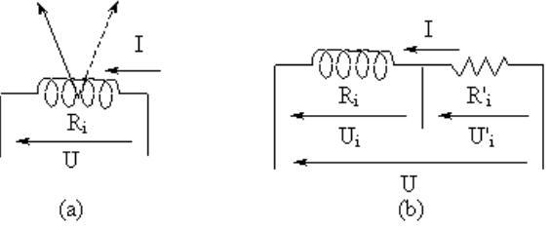
Figura 37 - Resistência adicional num voltímetro

Para 1 V o ponteiro deve deslocar-se para o final da escala o que corresponde a I = 1 mA. O valor de R equivalente à associação em série de R i e R' i obtém-se por aplicação da lei de Ohm:

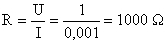
Sendo R = R i + R' i, o valor de R' i será R' i = R - R i = 1000 - 100 = 900 Ω. Diz-se que o campo de medida do aparelho é 1 V pois é o máximo valor da tensão que ele pode medir.

Resolução dos exercícios propostos no número anterior:

Exercício 5:

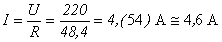
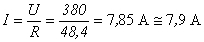
Exercício 6:

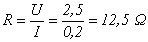
Exercício 7:

U = R I = 150 x 0, 02 = 3 V

Exercício proposto (Solução no próximo número):

Exercício 8

Pretende-se construir um voltímetro de acordo com o seguinte esquema eléctrico, em que A, B, C, D, E e F os pontos correspondentes aos vários campos de medida do aparelho e 0 é o ponto comum a todos os campos de medida. Cada medida é efectuada entre o ponto 0 (negativo) e um dos outros (positivo).

Já se sabe que o campo de medida correspondente ao ponto A é 1 V, sendo 1 mA o valor de I. Determinar os valores dos campos de medida correspodentes aos pontos B, C, D e E. Em seguida, determinar qual o valor que R''i deve ter para que o campo de medida de F seja 300 V.

 

AUTOR:Jorge Castilho Cabrita, Engenheiro Electrotécnico (IST), Professor do Ensino Secundário